|
|
1.IntroductionDiffuse correlation spectroscopy (DCS) is increasingly being used as a noninvasive method to quantify tissue blood flow, especially for neurological applications.1,2 DCS measurements quantify the temporal autocorrelation of fluctuations in the intensity of diffusely reflected light that has traveled through tissue. These fluctuations are almost entirely driven by the motion of red blood cells (RBCs) and thus by blood flow.2–4 Although DCS blood flow measurements have been validated against several alternative perfusion quantification methods,5–11 a discrepancy remains between the expected nature of RBC displacement and experimental results. Specifically, instead of an expected ballistic random flow with a uniform spatial velocity distribution,12 RBC motions measured by DCS have the characteristics of diffusive motion.4,13 Previous publications from our group13 as well as Ninck et al.14 hypothesized that DCS measurements are also sensitive to the shear-induced diffusion of RBCs in blood flow, a phenomenon previously observed through particle tracking experiments.15 Shear-induced diffusion refers to the random walk-like motion of particles in a shear flow due to interparticle hydrodynamic interactions. Although it was noted that the effective RBC diffusion coefficient is proportional to the flow shear rate, the question of what are the relative contributions of diffusive and convective motions to the observed intensity autocorrelation decay has not been addressed previously. In this publication, we seek to answer this question using Monte Carlo simulations of light scattering through tissues with varying densities and diameters of vessels. We explicitly model the location of each light scattering event within the vessel flow profiles and consider both convective motion and the corresponding shear-induced diffusion. Through these simulations, we obtain quantitative estimates of the contributions of both processes to the decay of the intensity temporal autocorrelation function. We present definitive evidence that diffusive motion dominates the decay for typical DCS experimental conditions and derive explicit expressions for the relationship between the measured RBC diffusion coefficient and absolute blood flow. Furthermore, we show that the commonly used DCS blood flow index derived using the correlation diffusion equation (CDE) for a semi-infinite geometry is directly proportional to absolute blood flow, but this proportionality is modulated by the hematocrit and the average vessel diameter in the volume of tissue probed by light. 2.Theory and Methods2.1.Correlation Diffusion EquationDCS measurements of blood flow are generally analyzed using the CDE.2,3 The CDE is derived from the correlation transfer equation (CTE)3,16 under the assumption that the probability of light scattering is much greater than the probability of light absorption, i.e., reduced scattering coefficient () is much greater than the absorption coefficient (). The CTE17 permits calculation of the electric field temporal autocorrelation function under more general conditions of photon migration. The CTE is similar to the traditional radiative transfer equation (RTE), which describes the propagation of light intensity through scattering media. The difference between the CTE and the RTE is that the CTE describes the propagation of the time-varying specific intensity, which represents an angular spectrum of the mutual coherence function. The temporal autocorrelation function is obtained as an integral of the time-varying specific intensity over all solid angles. Generally, an analytic solution of the CDE for a semi-infinite medium is used to fit the experimental measurements, i.e., where where is the reduced scattering coefficient, is the absorption coefficient, is the wavenumber of light in the scattering medium, is the probability of scattering from a moving scatterer, is the source–detector separation, , , , and given an index of refraction for tissue of 1.37.18It is customarily expected that the scatterer motion measured by DCS arises almost exclusively from RBCs. This is justified by experimental studies in animals, which showed that cessation of blood flow results in a nearly 100-fold reduction in the observed dynamics.4 In this paper, we will assume that RBCs are the only source of dynamic scattering events, and we will use instead of to denote the probability of scattering from an RBC. The mean square displacement (MSD) of the RBCs is generally given by where is the delay time, is the diffusion coefficient, and is the speed of the RBCs. Note that Eq. (3) can be expanded to use the Langevin formulation for diffusion,13,19,20 accounting for the diffusive motion velocity vector randomization that occurs at short-time delays.2.2.Monte Carlo SimulationsInvestigations with DCS have generally assumed that the motion of tissue scatterers is uncorrelated. Specifically, the assumption is that the phase shifts accumulated by the motions of scattering particles is uncorrelated, which depends on the motion of the scattering particle and the scattering angle. This assumption is generally valid when photons are scattering from particles undergoing Brownian motion. In the case of moving RBCs, this assumption is valid if the photon direction is randomized between scattering events from RBCs. This is true if the scattering is isotropic (i.e., the average cosine of the scattering angle is ) or if the photons scatter no more than once inside a vessel and the direction is randomized before scattering from another RBC in another vessel. The optical properties of blood at 800 nm indicate,21 however, that for a typical hematocrit of 40%, and the scattering length is , whereas the absorption length is over 250 times larger, at around 3.3 mm. Thus, photons entering any blood vessel larger than a capillary will most likely undergo multiple consecutive scattering events within the vessel with correlated linear motions of the RBCs. This breakdown of the uncorrelated motion assumption raises the possibility that the typically used solutions of the CTE, and thus the CDE, are not good models for analyzing DCS measurements of blood flow. To properly account for the effect of correlated motions on the decay of , we use Monte Carlo simulations of photon migration through highly scattering dynamic media and record details of the scattering angles for consecutive scattering events within vessels. Our Monte Carlo code is derived from what Boas originally utilized in Ref. 16 based on earlier work by Middleton and Fisher,22 Durian,23 and Koelink et al.24 The original Monte Carlo simulation propagates photons according to the scattering length and scattering anisotropy of the tissue, which we describe in more detail in Ref. 25. Photons are launched from a source position and recorded at discrete detector locations. For each detected photon, the total path length is recorded as well as the total dimensionless momentum transfer accumulated over all scattering events . The momentum transfer for a photon scattering event is given by , where and are the photon wavevectors scattered from and incident on the scattering center, respectively, and the total dimensionless momentum transfer is given by , where the sum is over scattering events. The temporal field autocorrelation function is then calculated by where is the number of photons detected, is the total dimensionless momentum transfer for photon , is the total path length of photon , is the absorption coefficient, and is the MSD of the scattering particles at a time delay of .The principal advance in the Monte Carlo simulations used in this paper is the introduction of blood vessels with different optical and dynamic properties than the surrounding tissue and with specified internal flow profiles, as shown in Figs. 1 and 2. Photon migration is simulated in a semi-infinite medium with the air tissue interface in the () plane at . The blood vessels share a common radius and are all oriented along the -axis with an even spacing in and of . The resulting translational symmetry allows for significant savings in the amount of memory needed to represent the tissue structure for the Monte Carlo simulation. We have verified that this preferred orientation of the vessels only introduces a small bias in our results compared to a truly random orientation of vessels, as expected, given that we typically simulate photons that have propagated a net-distance of several centimeters and have scattered hundreds of times. Fig. 1Simulation geometry used in this study. (a) Three-dimensional view and (b) () plane cross section. Vessels of radius are aligned with the -axis and are uniformly spaced in the () plane every . Photons are injected at a location within the () plane and detected a distance away. 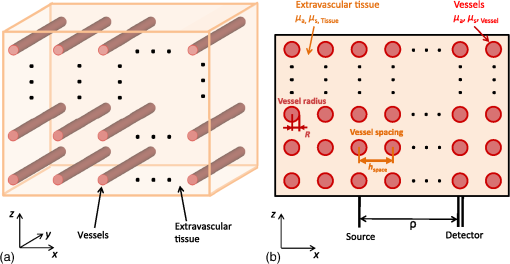 Fig. 2Photon propagation tracking. For each scattering event, we record the photon location and the magnitude of the momentum transfer . If the scattering event occurs inside a vessel, we also record the radial position and the component of along the vessel direction. In conjunction with a specified flow profile, the radial position determines the RBC convection velocity and the shear rate experienced by the RBC . 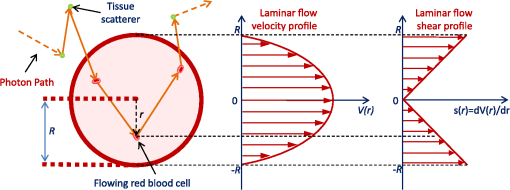 Photons are launched at a point on the surface along the -axis and are detected through a 2-mm-diameter circular aperture, a distance from the source point. Figure 2 shows a segment of a photon path and the parameters we record during the photon propagation. For each scattering step during the simulation, we explicitly test for the photon crossing the boundary of a cylindrical vessel. If a crossing occurs, the remaining propagation length for the scattering step is renormalized based on the new scattering coefficient as we describe in Ref. 25. For each detected photon, we record for every scattering event inside a vessel the index of the vessel, the radial position of the scattering event, the magnitude of the momentum transfer , and the component of along the vessel direction (-axis). Recording the vessel index enables us to determine consecutive scattering events within a vessel. Knowing the radial position of the scattering event permits us to consider a radial distribution for the convective and diffusive dynamics of the RBCs. We record the component of as it is needed to consider the correlated convective motion of the RBCs along the -axis. All Monte Carlo simulations in this paper use a source–detector separation of 2 cm, an () cross section of , and make use of translational symmetry to represent an infinite extent in . Each simulation run launches photons. To calculate the temporal field autocorrelation function, we start with the definition of and expand it to sum over all detected photons Note that one generally reports the normalized temporal field autocorrelation function , which is just normalized by the average intensity. The angle brackets indicate the ensemble average over scattering angles and particle displacements. The number of photons received at the specific detector is . The number of scattering events for the ’th detected photon is , where is the momentum transfer for the ’th scattering event of the ’th photon and is the displacement of the corresponding scattering particle at time lag . The total path length of the ’th photon in the ’th tissue type is given by and is the absorption coefficient of the ’th tissue type.We are considering the convective and shear-induced diffusive movement of RBCs such that the MSD of the RBCs is given by Eq. (3). Although the strength of the diffusive motion correlates with the magnitude of the local shear, the actual diffusive displacements are spatially uncorrelated with the convective displacements. Therefore, note that is generally much smaller than 1, and Eq. (5) can be rewritten as This formulation reveals the expected decay of due to the RBC displacements arising from diffusion and convective flow. Note that the decay arising from flow speed accounts for the correlated RBC displacements as the sum is performed over the consecutive scattering events of the ’th photon in the ’th vessel. The sum over the vessels entered by the ’th photon is outside the because the phase shifts are assumed uncorrelated between vessels, as the scattering angle and flow speed vector are generally randomized between photon interactions with different vessels. All of the information for calculating Eq. (6) is recorded by our Monte Carlo simulation. Given details about the RBC speed and shear-induced diffusion, we can now explicitly test which dominates the decay of and whether the CDE provides a good model fit and allows estimation of blood flow.2.3.Red Blood Cell Laminar Flow Profile and Shear-Induced DiffusionOur Monte Carlo simulations permit us to incorporate radial distributions for the flow speed and diffusion coefficient. A general form of the flow speed profile in vessels has been proposed to be26 where is the maximum speed at the center of the vessel, is the radius of the vessel, is a scale factor that allows for a nonzero velocity at the wall, and determines the degree of “bluntness” of the profile. In general, the smaller the vessel the more blunt the profile.26 For sufficiently large vessels, the flow speed profile can be considered to be laminar; thus, in our simulations, we only consider parabolic flow profiles with and . We believe this assumption captures the essence of the influence of the flow profile on RBC dynamic scattering events. If needed, other and values can be used in the future to account for the various degrees of flow profile blunting that have been observed in blood microrheology investigations.RBC dynamics, while flowing within a vessel, have been studied in numerous rheological studies including video microscopy to track the motion of RBCs ex vivo15 and whole blood in microchannels,27 as well as in vivo in rat venules.28 These studies have revealed that shear induces a diffusive behavior in the movement of the RBCs with the diffusion coefficient proportional to the shear rate, i.e., For our simulations, we use the value of from Goldsmith and Marlow.15Of note, a prior study by Wu et al.29 has shown that the gradient in the speed of scattering particles flowing within a channel can be the leading factor in the decay of the autocorrelation function. This is an informative study, but the parameters used are quite different from those encountered in biological tissue, leading to negligible levels of shear-induced diffusion. This is due to the use of a single flow channel with a much smaller shear rate than that experienced by RBCs in blood vessels, as well as a much smaller particle concentration and scattering coefficient. Furthermore, this study did not consider multiple flow channels in an otherwise static scattering medium. 2.4.Relating the Diffuse Correlation Spectroscopy Blood Flow Index to Absolute Blood FlowWe are now in a position to perform Monte Carlo simulations to calculate for RBCs flowing at varying speeds in vessels of varying diameters and spacings. We can then fit the result with obtained from the CDE to determine if the CDE remains a good model and to establish a quantitative relationship between the CDE blood flow index and the absolute blood flow . For a semi-infinite medium, we use given in Eq. (1) and estimate from Eq. (2). The optical properties and wavenumber of light are generally known in Eq. (2), leaving us to estimate . We define the blood flow indices and to be estimated by fitting either the convective or diffusive MSD model to , where either is expected to be linearly proportional to flow speed. The angle brackets for and are an explicit recognition that the measures the average speed or diffusion coefficient . Note that the probability of scattering from an RBC is not generally known a priori. In the context of photon diffusion theory, we would expect that is given by the product of the volume fraction of blood, and the ratio of the blood to average tissue reduced scattering coefficient, , i.e., The average tissue-reduced scattering coefficient is given by the volume fraction weighted average of the tissue and blood coefficients .We present results below for fitting . To establish the quantitative relationship between and for convective and diffusive RBC displacements independently, we obtain fitting results alternately setting and , respectively. We will distinguish these temporal field autocorrelation functions as and for convective and diffusive RBC displacements, respectively. In the case of convective motion only, we expect to be the spatially weighted average of RBC speed within the blood vessel. As the absorption length and photon transport length inside the vessel are generally larger than the vessel diameter, we expect uniform spatial sampling of the vessel and thus expect for a parabolic laminar flow profile. We thus arrive at an equation for In the case of diffusive motion only, we expect to be the spatially weighted average of the RBC diffusion coefficient within the blood vessel, i.e., given a parabolic laminar profile and uniform photon sampling of the blood vessel. We thus arrive at an equation for We define absolute blood flow as the volume of blood transiting through a unit volume of tissue per second, which is given by the flow in a vessel (cross-sectional area times average RBC speed) times the number of vessels per unit volume of tissue, i.e., where the number of vessels per unit volume of tissue in our geometry is We thus see that and Thus, the prediction from the CDE is that the blood flow index measured by DCS is proportional to absolute blood flow, but the proportionality is modulated by and . Additionally, the proportionality between and is further modulated by the number density of vessels. Note that we assume an estimate of from, for instance, an NIRS measurement or from a multidistance DCS measurement.30Finally, we present results below considering the combination of convective and diffusive RBC displacements to establish which dominates the decay of . Given the overwhelming indication from experimental studies,4 we expect to observe that the diffusive motion dominates the decay. 3.Results3.1.Impact of Scattering Length Within a VesselTable 1 summarizes representative optical properties of blood and extravascular tissue at 800 nm for a blood hematocrit of 40%.21 We use and the scattering coefficient in our Monte Carlo simulations. For the analytical solution provided by the CDE, we use the reduced scattering coefficient . Table 1Optical properties for blood and extravascular tissue at 800 nm.
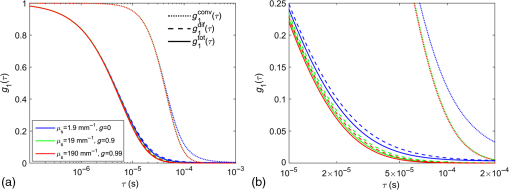
As a preamble, we explicitly test the prediction offered by the CDE that is invariant to changes in and provided that is constant. To this end, we ran Monte Carlo simulations for three different combinations of and maintaining a constant . Specifically, we use , 19, and , and , and 0.99, respectively. The rest of the optical parameters match the values in Table 1, except that we use and , which are typical values we use in our Monte Carlo simulations for the human head to accelerate the computation.25 We show results for -diameter vessels, spaced every , with . The results for and are shown in Fig. 3. These results confirm the prediction from the CDE that, at least for early decay times, is invariant as long as remains constant. The behavior at long decay times does exhibit some dependence on of the blood [see enlargement in panel b)]. Likely, as of the blood is decreased, the probability increases that a photon traverses a vessel without scattering from a moving RBC. Importantly, we observe that decays more quickly than , indicating that the shear-induced diffusion of the RBCs produces more dynamic fluctuations in the electromagnetic field than the flow speed convective displacements. Based on these results, for the remainder of the paper, we use since this gives us effectively the same results we would obtain with and leads to a more efficient execution of the Monte Carlo simulations. 3.2.Blood Flow Indices Estimated from Fitting Monte Carlo Data Using the Correlation Diffusion EquationIn this section, we present results to validate the relations for the blood flow indices and given by Eqs. (10) and (11), respectively. We do so by fitting the solution of the CDE, given by Eq. (1), to , obtained from the Monte Carlo simulations. As detailed in Table 2, we varied RBC speed, vessel radius, vessel spacing, and hematocrit in these simulations to fully test the dependencies of and on each parameter. Note that we fit to estimate and we fit to estimate . We only fit with the diffusion term because our simulations indicate that the dependence arising from the convective displacement of the RBCs has negligible impact on for our parameters of interest. For all cases presented in this section, the blood optical properties were , , and . For the tissue, we set , , and . Table 2Vascular parameter ranges explored in this study. Each parameter was varied separately while the others were held at a fixed value.
We first present results increasing the speed of the RBCs. Figures 4(a) and 4(b) show and the CDE fit for , and for and , respectively. In this example, the vessel diameter is set to , the vessels are spaced every 300 μm and the hematocrit is set to 40%. These results indicate that the CDE fits and well. Figures 4(c) and 4(d) show the fitted values of and versus speed, compared with those predicted using Eqs. (10) and (11). These results confirm that the s increase linearly with RBC speed and confirm the accuracy of Eqs. (10) and (11). Fig. 4(a) and (b) The CDE fit to the Monte Carlo results for and . The Monte Carlo results for different RBC speeds are indicated by the symbols and the diffuse equation fits are given by the colored solid lines. The symbols in (c) and (d) show the blood flow index determined from fitting with a diffusive motion model and from fitting with a convective motion model, respectively, versus the true RBC speed. The solid lines in (c) and (d) are the theoretical predictions for the s based on Eqs. (10) and (11). Here, we used 80 μm vessels spaced every 300 μm and set the hematocrit to 40%. 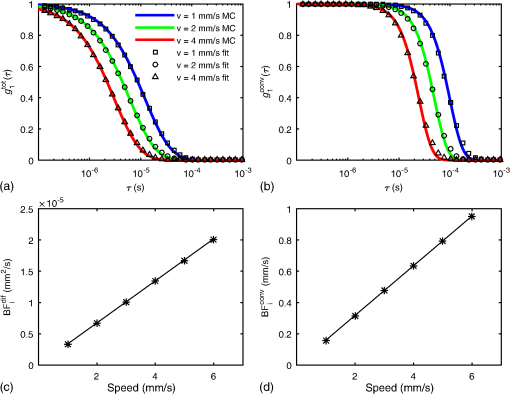 Figure 5 shows the fitting results for variations in the absolute volumetric blood flow achieved by varying the vessel diameter at a constant maximum RBC speed . The vessel diameter was varied from 30 to and results are shown for vessel spacings of 200 and 300 μm, respectively. As with the previous results, we fit and to estimate and , respectively. We then used Eqs. (14) and (15) to determine the expected values and find that this predicts well the measured . Fig. 5The symbols in (a) and (b) show the diffusive and convective blood flow indices, respectively, estimated using the CDE versus the true blood flow. The blood flow variation was accomplished by increasing the vessel diameter from 30 to with a fixed RBC flow speed of . The solid lines indicate the expected blood flow index values predicted by Eqs. (15) and (14), respectively. These results were obtained for a hematocrit of 40% 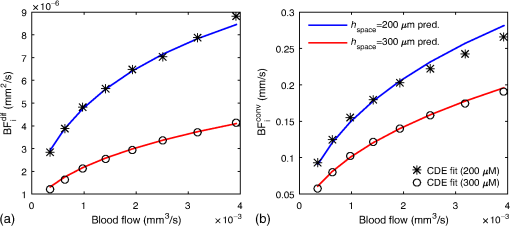 In Fig. 6, we plot fitted values for changing the blood hematocrit by from our baseline value of 40%. In this range, the reduced scattering coefficient of blood is changing linearly with hematocrit.21 We also show the expected values and find excellent agreement. Fig. 6The symbols in (a) and (b) show the diffusive and convective blood flow indices, respectively, estimated using the CDE for vessel scattering coefficients corresponding to hematocrit values ranging from to of our 40% baseline for a vessel diameter of , with vessel spacing, and an RBC flow speed of . The solid lines indicate the expected blood flow index values predicted by Eqs. (15) and (14), respectively. 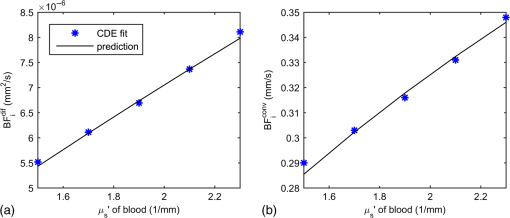 4.DiscussionThe agreement between the prediction by the CDE and the fits to the Monte Carlo results is striking. Despite the heterogeneous optical and dynamic properties of the vascular structure and the correlated consecutive scattering events within a vessel, the homogeneous solution of the CDE accurately describes the decay of . We have shown results fitting and , allowing us to test the convective and diffusive RBC displacement models for the CDE and demonstrate that the diffusive motion of RBCs dominates the decay of . Our fitting results confirm that Eqs. (14) and (15), which relate and to blood flow, are accurate within 5%. Importantly, while the CDE allows us to write a linear relation between the estimated blood flow index and true absolute blood flow, we see that the proportionality is modulated by the radius of the blood vessels and the reduced scattering coefficient of the blood (which is modulated by hematocrit). In the case of , the proportionality is further dependent on the number density of vessels. In this sense, it is fortunate that the diffusive motion of RBCs dominates the decay of ; thus, we do not need knowledge of the number density of vessels to estimate . Recall that the s depend on hematocrit even when absolute blood flow is constant because the s depend on the probability of scattering from an RBC, Eq. (9), which increases linearly with the reduced scattering coefficient of blood. Given that the diffusive motion of RBCs dominates the decay of , Eq. (15) thus stands as the quantitative relationship between the blood flow index measured by DCS and the true absolute blood flow. Recall that in order to get , we first need to know the average optical properties of the tissue and , which would generally be obtained from an independent NIRS measurement31,32 and possibly also estimated with multidistance DCS measurements.30 To then convert the to , we need to know the proportionality between shear flow and the RBC diffusion coefficient, the reduced scattering coefficient of the blood , and the radius of the blood vessels. In this paper, we used a value of obtained from Goldsmith and Marlow.15 We note that this is a value obtained for a hematocrit of 40% to 47% and that was found to linearly increase with hematocrit from 0% to 45% and then to plateau and reverse.33 The reduced scattering coefficient of blood is linearly proportional to hematocrit from 0% to 40%, the highest value measured by Meinke et al.21 In principle, if one has an independent measure of hematocrit, from a blood draw for instance, one can then determine the appropriate value to use for and . The remaining factor needed to estimate is the vessel radius . Although we performed simulations using vessels with a common radius, in reality DCS will measure vessels with a distribution of radii. We anticipate that Eq. (15) will still be valid when measuring a distribution of vessel radii, but that the effective vessel radius will represent a complex nonlinear dependence on the distribution of vessel radii and the corresponding RBC speed distribution. We note that in our previous publication,13 we postulated that the diffusional dependence of the DCS measurements in tissue arose because of sequential multiple scattering within a single vessel. As demonstrated in this paper, this factor does not play a major role in the interplay between diffusive and convective influences on the autocorrelation of multiple scattered light. Rather, it is simply that at source–detector separations commonly used for DCS measurements, the shear-induced diffusion dominates the signal. We estimate that the convective contribution only becomes significant when the detected photon path lengths become less than a millimeter, but this requires further investigation. A potential implication is that the convective contribution should be considered in analyzing laser speckle contrast imaging data.34 It is worth noting at this point that the concept of a well-defined absolute blood flow has been questioned as the value of absolute blood flow obtained has been theoretically demonstrated to depend on vascular geometry, measurement procedure, and spatial scale sampled.35,36 Further research is needed to better understand the implications of these theoretical arguments. 5.SummaryWe have presented a set of Monte Carlo simulations that quantify the contribution of diffusive and convective RBC motion to the decay of the autocorrelation function of light that has scattered through tissue. Through this modeling, we demonstrate that diffusive motion dominates the autocorrelation decay for typical experimental parameters used in DCS measurements. We have also provided expressions for the expected dependence of the measured DCS blood flow index on absolute tissue blood flow in terms of the vascular volume fraction, average vessel diameter, and blood optical properties. Our results indicate that the DCS blood flow index commonly obtained using the established CDE indeed offers a direct measure of tissue blood flow, but the proportionality is also sensitive to changes in hematocrit and in the average vessel diameter in the region probed by light. The immediate implication is that care must be taken to control for variations in these additional parameters when reporting DCS blood flow measurements. We expect further studies to explore these sources of variability and help define the range of effective DCS applications. AcknowledgmentsWe acknowledge financial support from the National Institutes of Health (NIH) Grants Nos. P41-EB015896, R01-NS091230, R21-NS093259, and R01-CA187595. ReferencesA. Torricelli et al.,
“Neurophotonics: non-invasive optical techniques for monitoring brain functions,”
Funct. Neurol., 29
(4), 223
–230
(2014). http://dx.doi.org/10.11138/FNeur/2014.29.4.223 Google Scholar
T. Durduran and A. G. Yodh,
“Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement,”
NeuroImage, 85
(1), 51
–63
(2014). http://dx.doi.org/10.1016/j.neuroimage.2013.06.017 NEIMEF 1053-8119 Google Scholar
D. Boas, L. Campbell and A. Yodh,
“Scattering and imaging with diffusing temporal field correlations,”
Phys. Rev. Lett., 75
(9), 1855
–1858
(1995). http://dx.doi.org/10.1103/PhysRevLett.75.1855 PRLTAO 0031-9007 Google Scholar
T. Durduran et al.,
“Diffuse optics for tissue monitoring and tomography,”
Rep. Prog. Phys., 73
(7), 076701
(2010). http://dx.doi.org/10.1088/0034-4885/73/7/076701 RPPHAG 0034-4885 Google Scholar
T. Durduran et al.,
“Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects,”
J. Biomed. Opt., 15
(3), 037004
(2010). http://dx.doi.org/10.1117/1.3425884 JBOPFO 1083-3668 Google Scholar
S. A. Carp et al.,
“Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring,”
Biomed. Opt. Express, 1
(2), 553
–565
(2010). http://dx.doi.org/10.1364/BOE.1.000553 BOEICL 2156-7085 Google Scholar
G. Yu et al.,
“Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,”
Opt. Express, 15
(3), 1064
–1075
(2007). http://dx.doi.org/10.1364/OE.15.001064 OPEXFF 1094-4087 Google Scholar
E. M. Buckley et al.,
“Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound,”
Opt. Express, 17
(15), 12571
–12581
(2009). http://dx.doi.org/10.1364/OE.17.012571 OPEXFF 1094-4087 Google Scholar
N. Roche-Labarbe et al.,
“Noninvasive optical measures of CBV, StO(2), CBF index, and rCMRO(2) in human premature neonates’ brains in the first six weeks of life,”
Hum. Brain Mapp., 31
(3), 341
–352
(2010). http://dx.doi.org/10.1002/hbm.v31:3 Google Scholar
M. N. Kim et al.,
“Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,”
Neurocrit. Care, 12
(2), 173
–180
(2010). http://dx.doi.org/10.1007/s12028-009-9305-x Google Scholar
C. Zhou et al.,
“Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,”
J. Biomed. Opt., 14
(3), 034015
(2009). http://dx.doi.org/10.1117/1.3146814 JBOPFO 1083-3668 Google Scholar
R. Bonner and R. Nossal,
“Model for laser Doppler measurements of blood flow in tissue,”
Appl. Opt., 20
(12), 2097
–2107
(1981). http://dx.doi.org/10.1364/AO.20.002097 APOPAI 0003-6935 Google Scholar
S. A. Carp et al.,
“Due to intravascular multiple sequential scattering, diffuse correlation spectroscopy of tissue primarily measures relative red blood cell motion within vessels,”
Biomed. Opt. Express, 2
(7), 2047
–2054
(2011). http://dx.doi.org/10.1364/BOE.2.002047 BOEICL 2156-7085 Google Scholar
M. Ninck, M. Untenberger and T. Gisler,
“Diffusing-wave spectroscopy with dynamic contrast variation: disentangling the effects of blood flow and extravascular tissue shearing on signals from deep tissue,”
Biomed. Opt. Express, 1
(5), 1502
–1513
(2010). http://dx.doi.org/10.1364/BOE.1.001502 BOEICL 2156-7085 Google Scholar
H. L. Goldsmith and J. C. Marlow,
“Flow behavior of erythrocytes. II. Particle motions in concentrated suspensions of ghost cells,”
J. Colloid Interface Sci., 71
(2), 383
–407
(1979). http://dx.doi.org/10.1016/0021-9797(79)90248-0 JCISA5 0021-9797 Google Scholar
D. A. Boas and A. G. Yodh,
“Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,”
J. Opt. Soc. Am. A, 14
(1), 192
–215
(1997). http://dx.doi.org/10.1364/JOSAA.14.000192 Google Scholar
B. J. Ackerson et al.,
“Correlation transfer—application of radiative transfer solution methods to photon correlation problems,”
J. Thermophys. Heat Transfer, 6
(4), 577
–588
(1992). http://dx.doi.org/10.2514/3.11537 JTHTEO 0887-8722 Google Scholar
R. C. Haskell et al.,
“Boundary conditions for the diffusion equation in radiative transfer,”
J. Opt. Soc. Am. A, 11
(10), 2727
–2741
(1994). http://dx.doi.org/10.1364/JOSAA.11.002727 Google Scholar
B. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Dover Publications, Mineola, New York
(2000). Google Scholar
K. Verdecchia et al.,
“Assessment of the best flow model to characterize diffuse correlation spectroscopy data acquired directly on the brain,”
Biomed. Opt. Express, 6
(11), 4288
–4301
(2015). http://dx.doi.org/10.1364/BOE.6.004288 BOEICL 2156-7085 Google Scholar
M. Meinke et al.,
“Empirical model functions to calculate hematocrit-dependent optical properties of human blood,”
Appl. Opt., 46
(10), 1742
–1753
(2007). http://dx.doi.org/10.1364/AO.46.001742 APOPAI 0003-6935 Google Scholar
A. Middleton and D. Fisher,
“Discrete scatterers and autocorrelations of multiply scattered light,”
Phys. Rev. B, 43
(7), 5934
–5938
(1991). http://dx.doi.org/10.1103/PhysRevB.43.5934 PRBMDO 1098-0121 Google Scholar
D. Durian,
“Accuracy of diffusing-wave spectroscopy theories,”
Phys. Rev. E, 51
(4), 3350
–3358
(1995). http://dx.doi.org/10.1103/PhysRevE.51.3350 Google Scholar
M. H. Koelink et al.,
“Laser Doppler blood flowmetry using two wavelengths: Monte Carlo simulations and measurements,”
Appl. Opt., 33
(16), 3549
–3558
(1994). http://dx.doi.org/10.1364/AO.33.003549 APOPAI 0003-6935 Google Scholar
D. Boas et al.,
“Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head,”
Opt. Express, 10
(3), 159
–170
(2002). http://dx.doi.org/10.1364/OE.10.000159 OPEXFF 1094-4087 Google Scholar
G. J. Tangelder et al.,
“Velocity profiles of blood platelets and red blood cells flowing in arterioles of the rabbit mesentery,”
Circ. Res., 59
(5), 505
–514
(1986). http://dx.doi.org/10.1161/01.RES.59.5.505 CIRUAL 0009-7330 Google Scholar
J. M. Higgins et al.,
“Statistical dynamics of flowing red blood cells by morphological image processing,”
PLoS Comput. Biol., 5
(2), e1000288
(2009). http://dx.doi.org/10.1371/journal.pcbi.1000288 Google Scholar
J. J. Bishop et al.,
“Effect of aggregation and shear rate on the dispersion of red blood cells flowing in venules,”
Am. J. Physiol. Heart Circ. Physiol., 283
(5), H1985
–H1996
(2002). http://dx.doi.org/10.1152/ajpheart.00888.2001 Google Scholar
X. L. Wu et al.,
“Diffusing-wave spectroscopy in a shear-flow,”
J. Opt. Soc. Am. B, 7
(1), 15
–20
(1990). http://dx.doi.org/10.1364/JOSAB.7.000015 Google Scholar
P. Farzam and T. Durduran,
“Multidistance diffuse correlation spectroscopy for simultaneous estimation of blood flow index and optical properties,”
J. Biomed. Opt., 20
(5), 055001
(2015). http://dx.doi.org/10.1117/1.JBO.20.5.055001 JBOPFO 1083-3668 Google Scholar
M. A. Franceschini et al.,
“Assessment of infant brain development with frequency-domain near-infrared spectroscopy,”
Pediatr. Res., 61
(5 Pt1), 546
–551
(2007). http://dx.doi.org/10.1203/pdr.0b013e318045be99 PEREBL 0031-3998 Google Scholar
F. Martelli et al.,
“Phantom validation and in vivo application of an inversion procedure for retrieving the optical properties of diffusive layered media from time-resolved reflectance measurements,”
Opt. Lett., 29
(17), 2037
–2039
(2004). http://dx.doi.org/10.1364/OL.29.002037 OPLEDP 0146-9592 Google Scholar
W. Cha and R. Beissinger,
“Evaluation of shear-induced particle diffusivity in red cell ghosts suspensions,”
Korean J. Chem. Eng., 18
(4), 479
–485
(2001). http://dx.doi.org/10.1007/BF02698294 Google Scholar
D. A. Boas and A. K. Dunn,
“Laser speckle contrast imaging in biomedical optics,”
J. Biomed. Opt., 15
(1), 011109
(2010). http://dx.doi.org/10.1117/1.3285504 JBOPFO 1083-3668 Google Scholar
R. Guibert et al.,
“On the normalization of cerebral blood flow,”
J. Cereb. Blood Flow Metab., 33
(5), 669
–672
(2013). http://dx.doi.org/10.1038/jcbfm.2013.39 Google Scholar
K. Kudo et al.,
“Quantitative cerebral blood flow measurement with dynamic perfusion ct using the vascular-pixel elimination method: comparison with h2(15)o positron emission tomography,”
AJNR Am. J. Neuroradiol., 24
(3), 419
–26
(2003). Google Scholar
BiographyDavid A. Boas is the director of the Martinos Optics Division in the Department of Radiology at Massachusetts General Hospital, and a professor of radiology at Harvard Medical School. He received his BS degree in physics at RPI and his PhD degree in physics at the University of Pennsylvania. He is the founding president of the Society for Functional Near-Infrared Spectroscopy, founding editor-in-chief of Neurophotonics, and the recipient of the 2016 Britton Chance Award in biomedical optics. Sava Sakadžić is a faculty member in the Optics Division of the Martinos Center for Biomedical Imaging at Massachusetts General Hospital and an assistant professor at Harvard Medical School. His research is focused on the development of optical microscopy technologies and their applications to study cortical oxygen delivery and consumption in normal brain and in various brain conditions. Juliette Selb is an instructor in the Optics Division of the Athinoula A. Martinos Center for Biomedical Imaging at Massachusetts General Hospital, Harvard Medical School. She received her PhD in 2002 from the Université Paris Sud in France for her work on acousto-optic imaging. Her current research focuses on diffuse optical modalities for brain imaging in humans. Parisa Farzam is a research fellow at Martinos Center at Massachusetts General Hospital, Harvard Medical School. She received her PhD in biomedical photonics from ICFO-The Institute of Photonics Sciences, Spain. Her research is focused on developing novel diffuse optical instrumentation, algorithms and protocols and applying them for preclinical and clinical investigations. Maria Angela Franceschini is a faculty member in the Optics Division of the Martinos Center for Biomedical Imaging at Massachusetts General Hospital and an associate professor at Harvard Medical School. Her research focuses broadly on the development and application of noninvasive optical techniques to studies of the human brain. She is a pioneer in the field of near infrared spectroscopy (NIRS) and has made substantial contributions to the modeling, testing, and clinical and neuroscience translation of NIRS and diffuse correlation spectroscopy. Stefan A. Carp is an assistant professor of radiology at Harvard Medical School and a member of Massachusetts General Hospital Martinos Center Optics Division. He received his BS degrees in chemistry and chemical engineering from MIT and a PhD from the University of California, Irvine, in biomedical optics. He focuses on the development of novel techniques for tissue hemodynamics and oxygen metabolism monitoring, as well as their translation to clinical use. |